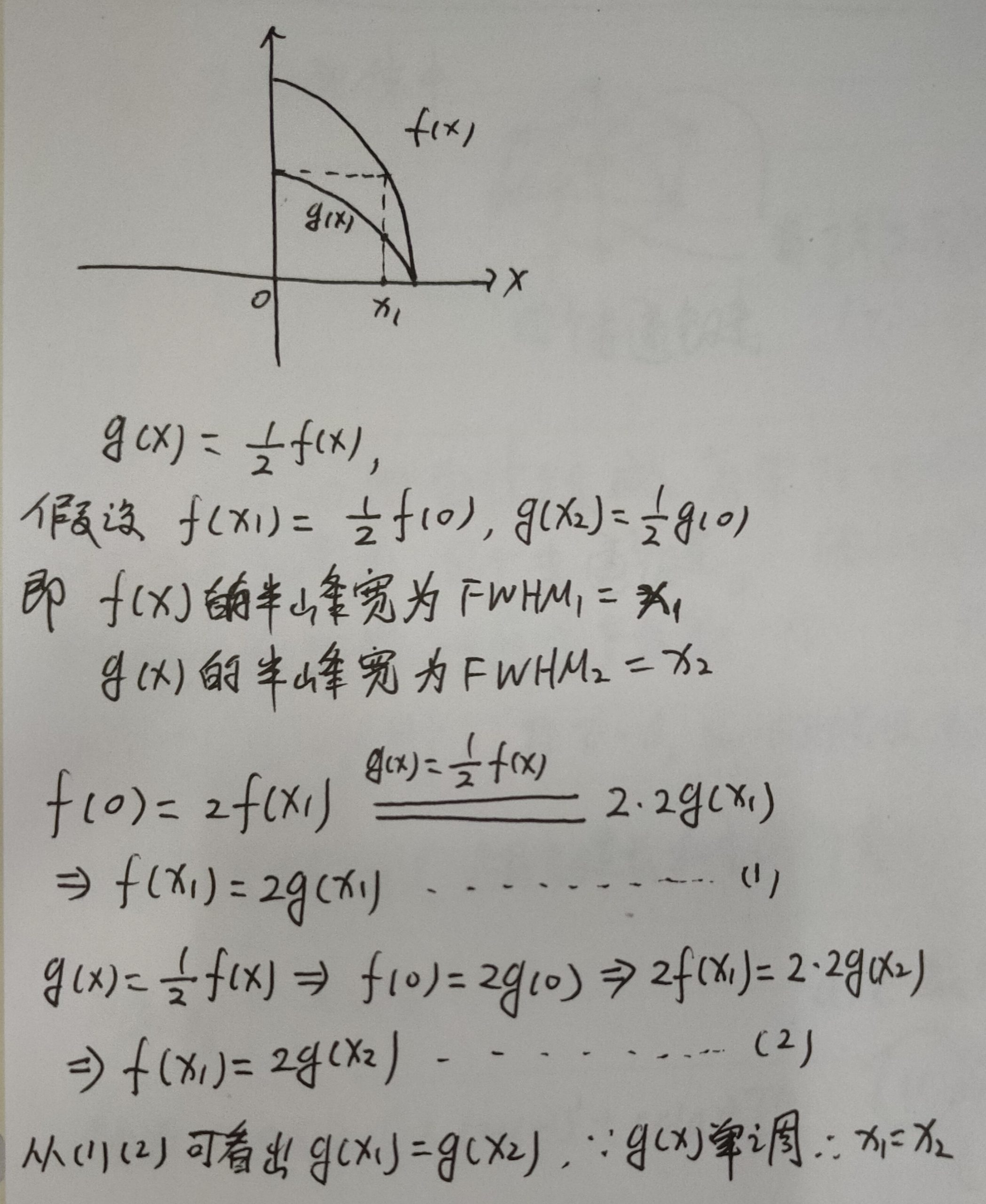
对于一个峰，我们总能以最高点所对应的横坐标将其分成左右两部分，f(x)是一个峰，g(x)是压缩后的峰，有g(x)=0.5f(x)，从图形中很容易看出压缩后的峰其半峰宽不会改变，因为g(x1)刚好等于0.5f(x1)，而g(x1)=0.5g(0)，所以当x1为f(x)的半峰宽是，同样x1也是g(x)的半峰宽。

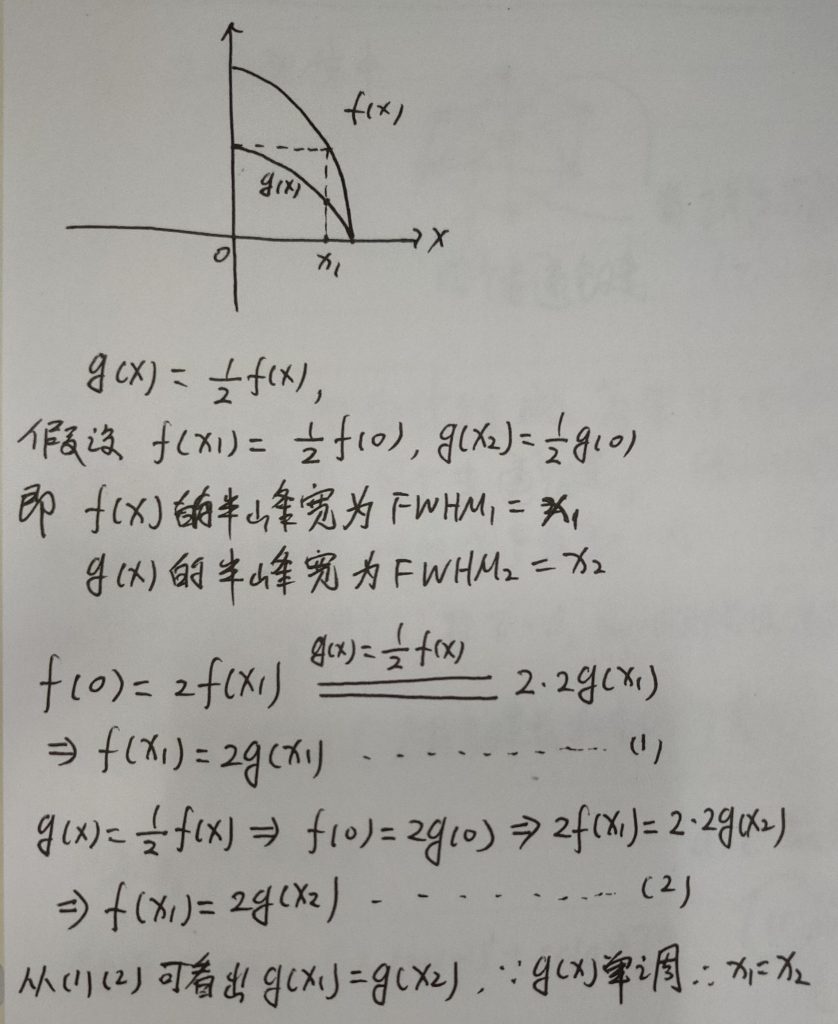
当然为了不失一般性，也可以假设f(x)=ng(x)+t，n不等于0，证法类似，如果t不为0，y=t是背景，不影响其半峰宽，算半峰宽是需要注意此时不应该是最大值的一半所对应的x值，而是最大值减去背景之后的一半所对应的x值，取t=0,只需要将上图中的（1）和（2）所对应的数字2改为n即可。

如果在这个过程中遇到了其它问题，欢迎在评论区留言，或者Google一下，也欢迎把具体的解决方法留在评论区，以供后来者参考

欢迎转载，不需注明出处，就说是你写的