氢离子在托卡马克装置的轨迹模拟

系统：Windows 10 专业版 1903
matlab版本：Windows版 2018a

使用说明

详细的推导过程见这篇文章， 程序需要用到这篇文章中的 Tokamak_Magnetic.m 程序 ， Plot_Plasma_Shape.m 为画圆截面等离子形状， Orbit_Boris.m 为模拟氢离子在托卡马克装置的运动。更改初始位置和速度即可模拟粒子运动轨迹，采用的Boris方法，程序运行比较久（几十分钟到几个小时），这跟你取的初始位置和速度有关，也可以减少程序中的n。

程序

Plot_Plasma_Shape.m

function Plot_Plasma_Shape(R0,a)
[u,v]=meshgrid(0:2*pi/50:2*pi,0:2*pi/50:1.5*pi);
X=(R0+a.*cos(u)).*cos(v); Y=(R0+a.*cos(u)).*sin(v);
Z=a*sin(u); mesh(X,Y,Z);axis equal;hidden off;colormap([0 1 1]);
xlabel('x');ylabel('y');zlabel('z');axis tight;
set(gca,'FontSize',20);
end

Orbit_Boris.m

tic;clc;clear
%choice=1，托卡马克（采用HL-2M）中氢离子运动，2：磁镜中氢离子运动
%需要注意初始位置和速度，r0：初始位置，v0：初始速度
%dt：时间步长，n：步数
choice=2;
if choice ==2
        c0=2e-7;R=0.2;I=1e6;L=2;
end
dt=1e-10;n=70000;
q=1.6e-19;m=1.6726231e-27;
r0=[0 2.2 0];v0=[0.5e7 sqrt(3)/2*1e7 0 ];
%r0=[0 0.00075 -1];v0=[0 sqrt(2)/2*1e6 sqrt(2)/2*1e5];磁镜
r(1,:)=r0;x=r(1,1);y=r(1,2);z=r(1,3);v(1,:)=v0;
%Boris算法实现步骤
for i=1:n
    v_minus=v(i,:);
    switch choice
        case 1
            [Bx,By,Bz]=Tokamak_Magnetic(r(i,1),r(i,2),r(i,3),3);   %3：HL-2M
            %如果能准备的给出安全因子的分布的表达式，速度可能会提高百倍。
           %[Bx,By,Bz]=Tokamak_Magnetic_S(r(i,1),r(i,2),r(i,3));
        case 2
            [Bx1,By1,Bz1]=magnetic(c0,R,I,r(i,1),r(i,2),r(i,3)+L/2);
            [Bx2,By2,Bz2]=magnetic(c0,R,I,r(i,1),r(i,2),r(i,3)-L/2);
            Bx=Bx1+Bx2;By=By1+By2;Bz=Bz1+Bz2;
    end
    B=[Bx By Bz];
    T=0.5*q*dt./m*B;
    S=2/(1+norm(T)^2)*T;
    v_zero=v_minus+cross(v_minus,T);
    v_plus=v_minus+cross(v_zero,S);
    v(i+1,:)=v_plus;
    r(i+1,:)=r(i,:)+v(i+1,:)*dt;
    p(i)=i;
end

%作图
figure(1)
plot3(r(:,1),r(:,2),r(:,3));hold on;
time=datestr(now,30);
if choice ==1
    R0=1.78;a=0.65; 
    Plot_Plasma_Shape(R0,a)
    savefig([num2str(r0),'_',num2str(v0),'_',time,'_','.fig']);
    figure(2);R0=1.78;b=sqrt(r(:,1).^2+r(:,2).^2);
    plot(b,r(:,3));
    xlabel('rho');ylabel('z');set(gca,'FontSize',20);
    axis equal
    savefig([num2str(r0),'_',num2str(v0),'_',time,'_r_z_','.fig']);
end
if choice==2
    savefig([num2str(r0),'_',num2str(v0),'_mirror_',time,'_.fig']);
end
% figure(3)  %能量守恒较好
% p(i+1)=i+1;
% plot(p*dt,sqrt(v(:,1).^2+v(:,2).^2+v(:,3).^2));
%set(gca,'FontSize',20);xlabel('t');ylabel('v');
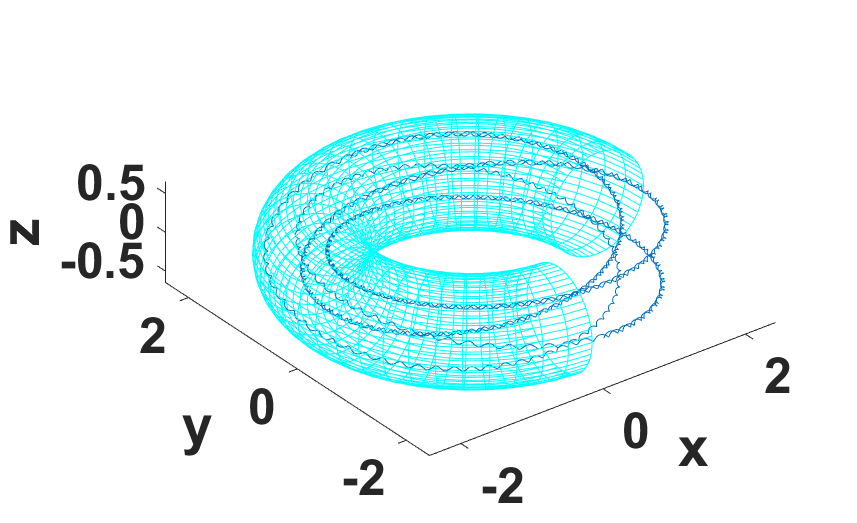
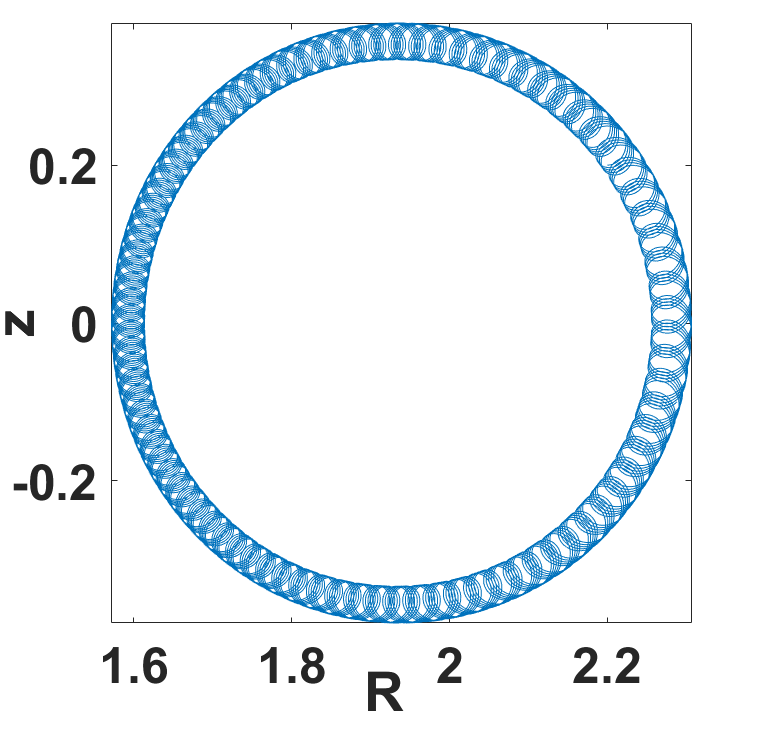
toc

通行粒子轨迹和极向投影（模拟的HL-2M中的氢离子）

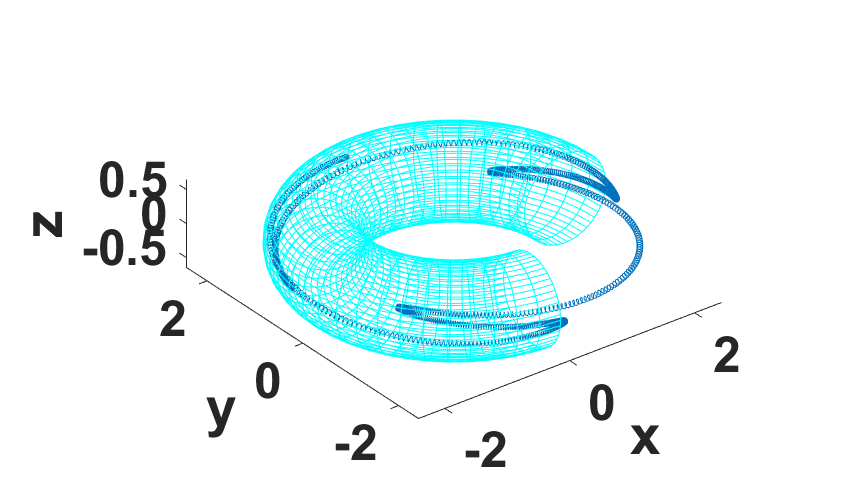
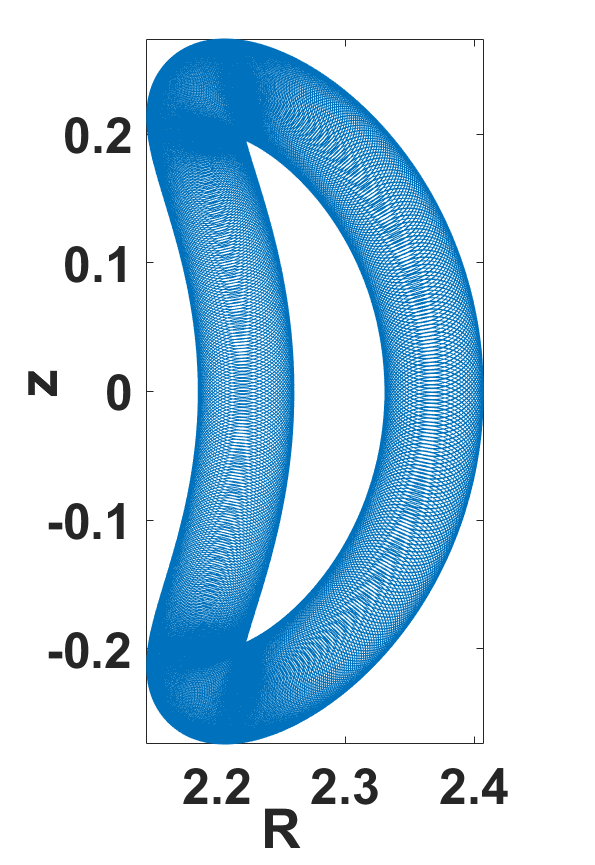
捕获粒子及其极向投影

源码

欢迎转载，不需注明出处，就说是你写的